L D[AR2P#0.0]
Lifetime Supporting Member
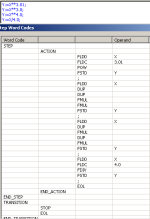
The S7 coding for the initial guess is as follows: (from Kahan, see interesting ref http://www.cims.nyu.edu/~dbindel/class/cs279/qbrt.pdf)
The initial guess for the cubed root of 15625 is 25.57 (as in Peter's previous post)
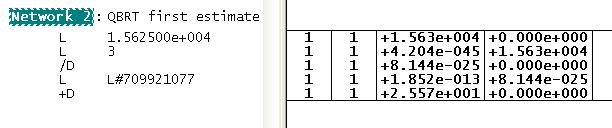
The initial guess for the cubed root of 15625 is 25.57 (as in Peter's previous post)

Last edited: