MaxK
Member
#116 #125
Are you sure that is what destination unknown is using?
Guess we should ask Destination Unknown about it
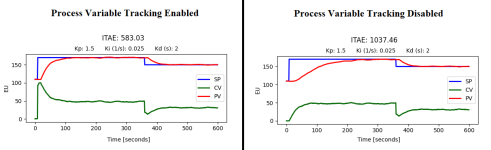
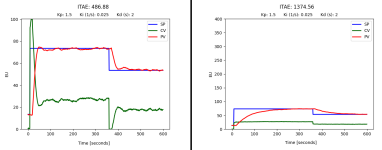
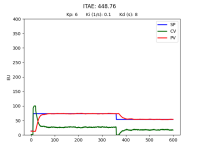
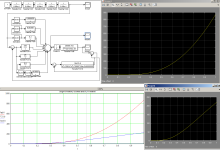
Could you please point out the differences between the system shown in the block-diagram (below) and the system in your video?
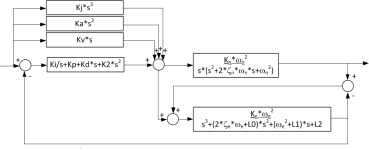
Are you sure that is what destination unknown is using?
Guess we should ask Destination Unknown about it
Use software/modeling. My estimated positions are better than the feed back positions on a sample to sample basis.
https://www.youtube.com/watch?v=7Gmrc-dj_uc&t=14s
Could you please point out the differences between the system shown in the block-diagram (below) and the system in your video?