I can also tune without a model. But practice has shown that this is not the most ideal method. This is because tuning is time-consuming and (sometimes) expensive (especially with slow processes). Just doing a step response and getting a model out of it is much more interesting.
+1000
In the attachment, I have done a plot. This plot has been accelerated 200 times. I can enter this speed myself.
This isn't clear too me.
The negative D-factor is certainly interesting! I am going to take a look at this.
Try my controller parameters in you simulator just like I tried your controller parameters in my simulator.
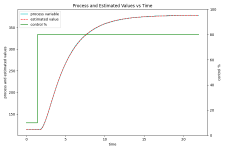
This is my results to the "hotrod.txt" data. I am computing a SOPDT model. The process variable is the actual recorded data. The estimated value is is generated by my model from the system identification.
If the estimated and process values are close to the same then my model is good.
final_simplex: (array([[ 3.75738871, 0.68459748, 2.8492896 , 77.84212178, 0.35403269],
[ 3.75738895, 0.68459766, 2.84928924, 77.8420959 , 0.35403266],
[ 3.75738776, 0.68459769, 2.84928958, 77.84219321, 0.35403292],
[ 3.75738878, 0.6845977 , 2.84929003, 77.84211757, 0.35403232],
[ 3.75738864, 0.68459843, 2.84928914, 77.84212303, 0.35403212],
[ 3.75738929, 0.68459787, 2.84928892, 77.84207222, 0.35403256]]), array([250.31411453, 250.31411796, 250.31413401, 250.31413445,
250.31413467, 250.31421152]))
fun: 250.31411452756277
message: 'Optimization terminated successfully.'
nfev: 204
nit: 105
status: 0
success: True
x: array([ 3.75738871, 0.68459748, 2.8492896 , 77.84212178, 0.35403269])
RMS error = 0.436
The open loop gain = 3.757 PV/%CO
Time constant 0 = 0.685 minutes
Time constant 1 = 2.849 minutes
Ambient PV = 77.842 in PV units
Dead time = 0.354
Time units are the same as provided in input file
The closed loop time constant = 0.285
The controller gain = 1.472 %CO/unit of error
The integrator time constant = 3.534 minutes
The derivative time constant = 0.552 minutes