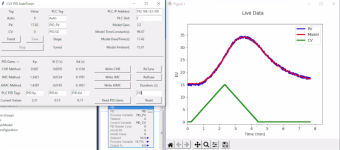
I have an older version of my autotuner here
https://deltamotion.com/peter/py/SysID SOPDT.zip
It has Ron Beaufort's "HotRod" data for an example problem.
The code can use 3 methods to minimize the error between the actual and estimated response.
Nelder-Mead is the one I use. Powell's method works OK too. BFGS should be the best, but it has problems. It keeps quitting too early due to resolution problems. BFGS seems to work great if given a perfect mathematical model but not with real data. I have spent a lot of time comparing these problems. Nelder-Mead always works.
Destination Unknown and I could put those making auto tuners out of business.
I think if I trained 10 people, we could tune all the systems in North America remotely.
Destination Unknown could find 9 more missing persons, train them, and tune all of the EU.
Something similar could be done for Asia.
The Nelder-Mead/Downhill Simplex/Amoeba method is not only simple, N-M works when other methods fail. The reason is that the Nelder-Mead method doesn't rely on finding derivatives or slopes.
Before the CCP-virus I was working on a method of computing the x, y, x and yaw, pitch and roll of a Six Degree of Freedom platform (6DOF). Each of the 6 cylinders had an analog/resistive feedback but they were noisy. The x, y, z and yaw, pitch and roll would never converge because of the noisy feedback, so I had to use a method that didn't use derivatives or slopes.
Now that computing power and algorithms are plentiful, there are no more excuses for running systems in manual or poorly tuned systems.
Here is an example where a simple PID will not work Controllers like the HYD02, M02AS and RMC100 will fail on this system.
https://deltamotion.com/peter/Videos/NF-FOA.mp4
Some on this forum have had a chance to tune this system as part pf an advanced training class. It was designed to be purposely difficult to tune. The auto tuners presented so far would all fail on this system. PID does not work all the time. Think about how you would control the position of the end of a slinky with dead time.