Peter Nachtwey
Member
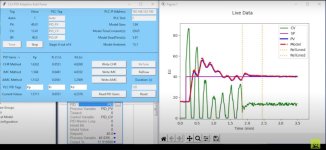
OK, now I see that the engineering units are Hz. I like Hz over RPM too only I usually say revolutions per second or rps.
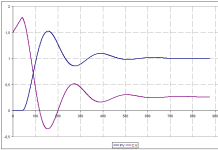
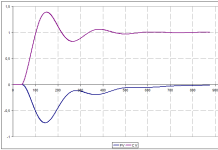
Another question I have is why does the model start at about 27 Hz instead of zero like the PV?
Also, I can see that the controller is not controlling the speed directly. There must be a drive in between the controller and the motor. In torque or current mode the torque/ angular acceleration is proportional to the current to the motor. Your system appears to be in velocity mode where the velocity is proportional to the voltage to the drive.
When tuning a motor in velocity mode we usually excite the motor with an output that looks like a W or M depending on the direction. When tuning is torque mode we output a pulse that stays on until the motor reaches a desired speed or travels a distance limit and then we must brake by outputting a negative pulse to decelerate. We usually get better performance by skipping the velocity loop inside the drive.
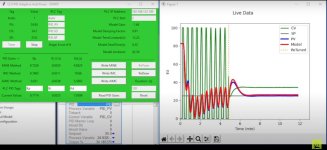
Another question I have is why does the model start at about 27 Hz instead of zero like the PV?
Also, I can see that the controller is not controlling the speed directly. There must be a drive in between the controller and the motor. In torque or current mode the torque/ angular acceleration is proportional to the current to the motor. Your system appears to be in velocity mode where the velocity is proportional to the voltage to the drive.
When tuning a motor in velocity mode we usually excite the motor with an output that looks like a W or M depending on the direction. When tuning is torque mode we output a pulse that stays on until the motor reaches a desired speed or travels a distance limit and then we must brake by outputting a negative pulse to decelerate. We usually get better performance by skipping the velocity loop inside the drive.