I didn’t find it there.
Did it myself. Please find it at attached xls file.
That is NOT the way to do it.
To do what? To use high order derivates instead dead time? Why? I have no reason to suppose that the real plant includes significant "dead times".
I have posted how to do it many times. I don't know why I bother if no one pays attention. I will post it again.
https://deltamotion.com/peter/Mathcad/SOPDT/Mathcad - SOPDT_HOTROD.pdf
Thanks.
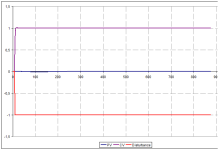
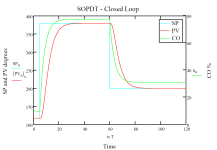
1. You and I have a different meaning of the term "ideal loop". Please find curves of "ideal loop" step disturbance response below.
2. The document provides a good formula for calculating the PID controller arguments to get a "nice and smooth" change-setpoint-response curve, not so "nice and smooth" for disturbance response.
Let’s look at the CO curve on the last page (I've attached the image below)
At 5-th minute setpoint changes from 117,6 to 380.
Before 5-th min CO =10 i.e. Ui = 10. Kc = 0.23675.
At first iteration (PLC scan) after setpoint changes
Error value E = setpoint – actual PV = (380 – 117,6) = 262,4
CO = Kc*E + 1/Ti *E*dt + Ui(-1) + Td* (E – E(-1))/dt = 0,23675*262,4 + 1/3,6 * 262,4 * 1/60 +10 + 0,557*(262,4-0)*60 = 8842,75
At second iteration (PLC scan) after setpoint changes
CO ≈ 0,23675*262,4 + 1/3,6 * 262,4 * 1/60 +10 + 0,557*(262,4-262,4)*60 = 73,34
What I see in the picture is somewhat different from the above calculations. Won't you explain?
You can't properly place the closed loop poles with the derivative gains.
Let's play “captain obvious”!
If real plant includes dead time you right!
If the real plant doesn't include dead time, you're still right! - it is impossible to completely describe a real plant using LDE, so the roots of the equation will never fully respond real plant.
Peter, I'm not native speaker. My English quite poor. And of course I don't feel language overtones.
“What??” – I don't get what it actually means.
No one does but you shouldn't use it as an excuse. If the model is accurate within 5% that is pretty good if you use feed forwards/bias. The feed forwards will then get close and the closed loop control only needs to do the remaining 5% This would reduce the error by a factor of 20. I usually can get within 2%.
I do not evaluate the accuracy of models because I do not know how.
You can use trial and error. I try to place the closed loop poles on the negative real axis so the error decays without overshoot. Overshoot is bad in motion control applications.
As I noted earlier, I take into account the ratio of the imaginary and real parts of the roots of the characteristic equation.