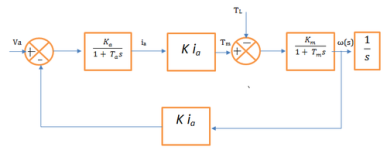
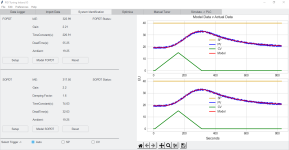
I've attached block diagram of separately excited DC motor with armature control.
I don't know the exact circuitry of your amplifier, but I think it also has a some order transfer function.
So I think actual model is little bit more complicated
Yes, it is probably more complicated, I don't think my model is exactly right. Accelerations should be integrated twice to get position, not once. However, the delay is so small it can be assumed to be zero. I have no documentation on the motor and the amplifier. When I go into the field the customer doesn't either so I must rely on making a model.
????
The amplifier "converts" the control signal into voltage pulses.
Voltage gets converted to current by motor armature.
Ia = (Va - Eb)/Ra
You are trying to model what is inside the amplifier when there is no documentation or feed back.
In other words:
We can only say that we have an LDE (or something), witch response to some influence (change setpoint, disturbance) differs from the response of the plant to some SSE (or something). And this is correct for some range of the plant states.
Actually a couple of linear differential equations. One for velocity and another to integrator velocity to position.
All in all. What was the reason to show me this movie?
Do you think I don't know that 99% for PID-tuning use simplified models?
Actually, no. Your examples in the past have been for non-integrating systems.
Do you think I do not know that in 99% of cases the result is acceptable?
So why did you complain about models not being accurate above?
But tell me this. In what percentage of cases, after the drift of plant parameters and the subsequent crash of the system,
Why should this happen? I have a video where I use this to tune a 250 HP rotary clipper. It has been working for 16 years now.
does the tuner scream that the PID controller has gone crazy because he (tuner) tuned it for an "accurate model" and "it was working good" but something mysterious happened?
No, the tuner isn't always on-line and doesn't scream.
BTW, your diagram is wrong. The feed back is position and should come from after the 1/s because the feed back is position, not velocity. The reference should be a target position that is compared with the feed back or actual position.
The target position should be differentiated once to get the target velocity. The target velocity is multiplied by the velocity feed forward and summed after the PID ( where is the PID? ). The target position is differentiated twice to get the target acceleration. The target acceleration is multiplied by the the acceleration feed forward and summed with the PID and velocity feed forwards. This value goes to the amplifier.
We don't know what is happening after that. There is no feedback from inside the amplifier. If there was then we could implement an inner loop but the only feed back is the encoder position.
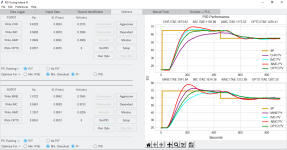
If you look carefully at the video you can see values for the PID and the two feed forwards when I move the slider up. The slider is placing the closed loop poles on the negative real axis is the s domain. As I move the slider bar up it is effectively moving the closed loop poles to the left. This makes errors decrease faster. Keeping the closed loop poles on or close to the negative real axis also avoids or minimizes over shoot. Also, if the plant parameters should change, the closed loop poles will still be close to the negative real axis and far from the origin so the system remains stable. I do tests for this by randomizing the plant parameters with a standard deviation of 10% and check the responses. This means a parameter has a 1% chance of changing by 30%. My models are never off this much.