Peter Nachtwey
Member
In reality EVERYTHING HAS A DEAD TIME!!!!I please to excuse me, I have one stupid question:
Why do all your models include dead time? Do all your systems have transport delay (conveyors, pipelines, etc.)? What is the reason?
In most cases the dead time is so small it can be ignored.
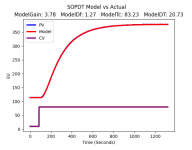
That doesn't' look right because there is no dead time. What is the SSE ( sum of squared errors ) between the actual data and your estimated data? I always print that because it tells me how good my model is.Peter Nachtwey's "Hotrod.zip" example is approximated pretty well by the following function
W(s) = 3,77142857142857/ ((170,2864769*s+1)* (36,0195267*s+1)* (14,57362541*s+1)* (11,51468826*s+1))
This doesn't look right either. Again, would like to see the SSE.destination unknown example (post 36):
W(s) = 2,22 / ((91,225*s+1)* (21,3625*s+1))
(If I get data (not image) maybe I can improve the model.)
SSE is the sum of squared errors is more appropriate than other evaluation methods when testing for goodness of fit between a model and actual data.
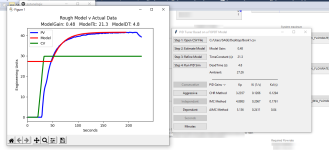
My SOPDT program returns this for hotrod.txt
sse = 250.31414761879358
RMS error = 0.436
The open loop gain = 3.757 PV/%CO
Time constant 0 = 0.685 minutes
Time constant 1 = 2.849 minutes
Ambient PV = 77.840 in PV units
Dead time = 0.354
Time units are the same as provided in input file
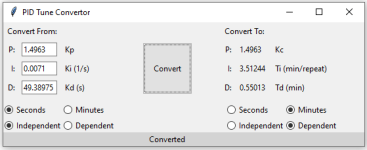
The closed loop time constant = 0.285
The controller gain = 1.472 %CO/unit of error
The integrator time constant = 3.534 minutes
The derivative time constant = 0.552 minutes