sse = 250.3141656165739
sse = 250.31416493541923
sse = 250.31414761879358
final_simplex: (array([[ 3.75741204, 0.68461421, 2.84927027, 77.84024028, 0.35401924],
[ 3.75741276, 0.68461511, 2.84926905, 77.84016508, 0.35401852],
[ 3.75741085, 0.68461181, 2.84927089, 77.84033032, 0.35402135],
[ 3.75741199, 0.68461453, 2.84926966, 77.84023678, 0.35401922],
[ 3.75741296, 0.68461419, 2.84927032, 77.8401676 , 0.35401904],
[ 3.75741189, 0.68461419, 2.84927023, 77.84025638, 0.35401937]]), array([250.31414491, 250.3141476 , 250.31414762, 250.3141638 ,
250.31416494, 250.31416562]))
fun: 250.31414490854445
message: 'Optimization terminated successfully.'
nfev: 764
nit: 452
status: 0
success: True
x: array([ 3.75741204, 0.68461421, 2.84927027, 77.84024028, 0.35401924])
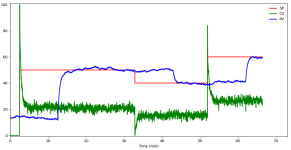
printing plot
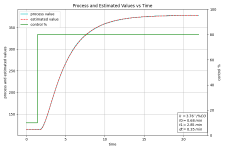
RMS error = 0.436
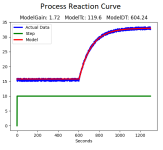
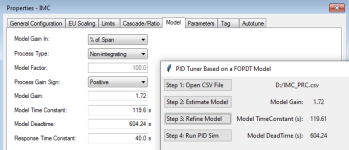
The open loop gain = 3.757 PV/%CO
Time constant 0 = 0.685 minutes
Time constant 1 = 2.849 minutes
Ambient PV = 77.840 in PV units
Dead time = 0.354
Time units are the same as provided in input file
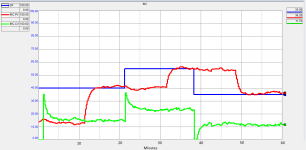
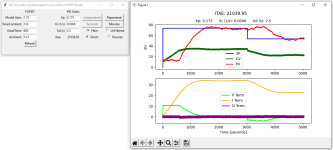
The closed loop time constant = 0.285
The controller gain = 1.472 %CO/unit of error
The integrator time constant = 3.534 minutes
The derivative time constant = 0.552 minutes